Criteria of Maxima and Minima

Criteria of Maxima

The followings are the criteria of maxima of a function.

(i)  The derivative  dy/dx is + ve just before x = a and – ve just after it.

(ii)  The derivative  dy/dx = 0, just at the point x = a, since it can change its sign from + ve to –ve by passing through zero only.

(iii) The derivative dy/dx is a decreasing one, since it changes sigh from + ve to – ve. This means  d²y/dx< 0.

Criteria of Minima

The followings are the criteria of minima of a function.

(i) The derivative dy/dx is = ve just before x = a and + ve just after it.

(ii) The derivative, dy/dx is equal to zero just at the point x = 0, since it can change its sign from – ve to + ve by passing through zero only.

(iii) The derivative dy/dx is an increasing one, since it changes its sign from –ve to + ve. This implies that d²y/dx² >0.

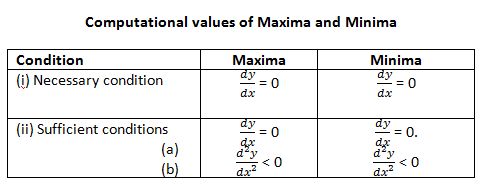
From the above criteria of maxima and minima of a function, their computational values may be tabulated as follows: