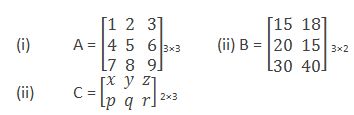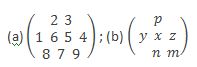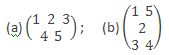Matrix
A matrix may be defined as an orderly arrangement of some numbers and symbols in certain rows and columns enclosed by some brackets, subscripted by the magnitude of its order and denominated by some capital letter.
Essential Characteristics
From the above definition and the specimens, the essential characteristics of a matrix may be analysed as under:
(i) It consists of some numbers or symbols. The numbers like, 0, 5, 10, 125, 3500 and the symbols like x,y,z etc. constitute a matrix. These are called the elements of a matrix without which a matrix cannot come into existence. These numbers may take any sign and any form like ± fractions like 3/7, – 2/11, – 7/9 and ± integers, ± decimals like .35, – .75, ± fractions like 3/7, – 2/11 and ± mixed numbers like, 10,75, – 3.375 etc, They may consist of single digits or multiple digits including only zeroes even. However in order to constitute a matrix, they must be orderly arranged in some rows and columns. Any disorderly scattered numbers, or numbers and symbols will not amount to matrices:
Further, the elements should be so arranged that each of them is capable of being subscripted by its ith row and jth column to locate its position in the matrix. Thus, if an element say, 15 is subscripted as 151.2, it would indicate that the said element 15 lies in the first row and second column of the matrix. In a disorderly arrangement of numbers like the above ones a number cannot be subscripted by its ith row and jth column.
(ii) It Consists of some rows and columns. A matrix always consists of certain rows and columns in which all its elements are arranged. The number of such rows and columns may be one or more and there may or may not be equality between the number of rows and the number of columns. But a columns or a row must be complete with some elements. Thus a group of rows and columns not completed with all its elements as follows will not amount to a matrix:
It may be noted that an empty space in a row a column is not equal to ‘0’ for that a ‘0’ is an element, where as an empty space is never an element of a matrix.
(iii) It must be enclosed by some brackets. A group of orderly arranged numbers or symbols to be called a matrix must be enclosed by some brackets viz. parentheses ( ), square brackets [ ], or curly bracket { }, However, conventionally, the curly brackets are not used in representing a matrix. Thus, a groups of following numbers and symbols not encompassed by any bracket will not constitute a matrix.
(a) 1 2 3 (b) x y z
4 5 6 m n p
(iv) It must be subscripted by the magnitude of its order. The magnitude of the order of a matrix refers to the number of rows and column with which a matrix is constituted. The number of rows and columns must be subscripted at the end at the bottom of the right hand side bracket of a matrix as m × n (read as m by n), where m, represents the number of rows and n the number of columns in the matrix. Thus, in a matrix, if the subscript stands like, 4 × 3, it will mean that there are 4 rows and 3 columns in the said matrix.
(v) It must be denominated by some capital letter. Every matrix must be denominated properly for making a reference to it in the course of computational works. Conventionally, all the matrices are denominated or named by some letters of upper case viz. A, B, C, D etc. Without the proper denomination, any orderly arrangement of numbers or symbols will not constitute a matrix. Having thus, analysed the whole corpus of a matrix may be represented as under:
Where, A refers to the name of the matrix, e to the element or entry in the matrix ‘ i. j. to the subscript of an element in which i, indicates the row and j the column of the matrix in which the element appears ; m × n, to the subscript of the matrix in which m indicates the numbers of rows and n the number of columns contained in the matrix and ( ), to the enclosure or boundary of the matrix.