Maximum and Minima
A function f(x) is said to be maximum (i.e. has attained its maximum value) at a point, if the function cases to increase and begins to decrease at that point. Symbolically, it can be represented as f(a) ≥ f(a+ h), where, h is the sufficiently small increment and a is the point to which f(x) approaches.
On the other hand, a function, f(c) is said to be minimum (i.e., has attained its minimum value) at a point, if the function ceases to decrease and begins to increase at that point. Symbolically, this can be represented as f(a) ≤ f(a + h) where, h is the sufficiently small increment and a is the point to which f(x) approaches.
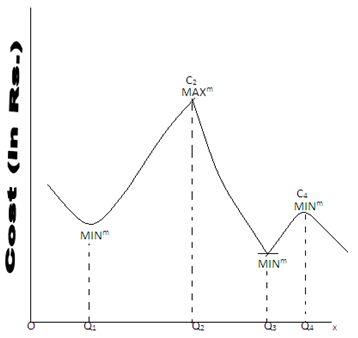
The concept of maxima and minima of a function will be made more clear from the following graphs.
From the above graph it must be noticed that the points c1 and C3 are the minimum and the points C2 and C4 are the maximum points of the graph. The function f(x) has maximum values Q2C2 and Q4C4 when x = OQ2 and OQ4 respectively. On the other hand, the function f(x) has maximum values Q1C1 and Q3C3 when x = OQ1 and OQ3 respectively.