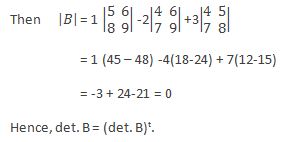Properties of a Determinant
The determinants have a good number of algebraic properties which help us in finding the numerical values of the determinants at an ease and straight away. Besides, they also help us in applying the elementary operations over the rows and columns of a determinant to simplify its form and arrive at the value at a quicker rate. These properties hold good for the determinants the value at a quicker rate. These properties hold good for the determinants of any order but we shall probe them to the bottom only with the determinants up to the order 3. Some each, important properties are enumerated here as under:
1.The value of a determinant becomes zero if any row or column of the some consists of zeroes only
4. If any two adjacent rows or columns of a determinant are interchanged, the numerical value of the determinant remains the same but with the opposite sign.
Let the determinant of order 3 be
Hence, in all the above cases it is proved that by the interchange of any two adjacent rows or columns the value of the determinant remains the same but with the opposite sign.
6. If the elements of any row or column of a determinant are multiplied in order by the co factor of the corresponding elements of any other row or column, then the sum of the products thus obtained is zero.
Now, multiplying the elements of the by the co factors of the responding elements of the and getting them summed up we get,
4 × 2 + 5 × -2 + 1 × 4 = 6-10 + 4 =0.
Hence, from the results of all the above examples the property of the determinant thus cited is proved.
7. The value of the determinant remains unchanged, if to each element of any particular row or column of the determinant is added or subtracted the equimultiple of the corresponding elements of one or more rows or columns.
Hence, in all the above examples, the property of the determinants cited above holds good.
8. If each element in a row a column of a determinant is multiplied by a constant K, then the value of the determinant gets multiplied by the same constant K.
= -60 -180 + 375 = 135 = 5(27)
9. If every element in any two or column consist of the sum or difference of two quantities, then the difference of two quantities, then the determinant can be expressed as the sum or different of two determinants of the same order:
Let the determinant of order 3 be
Now, the co factors of the elements of R2 are:
Multiplying the elements of the R2 by their corresponding co factors thus obtained and getting them totaled we get,
5 × 3 -3 + 4 × -52 + 2 × 21 = -15 -208 +42
= -223 + 42 = -181
Hence, the given property of the determinants is established.