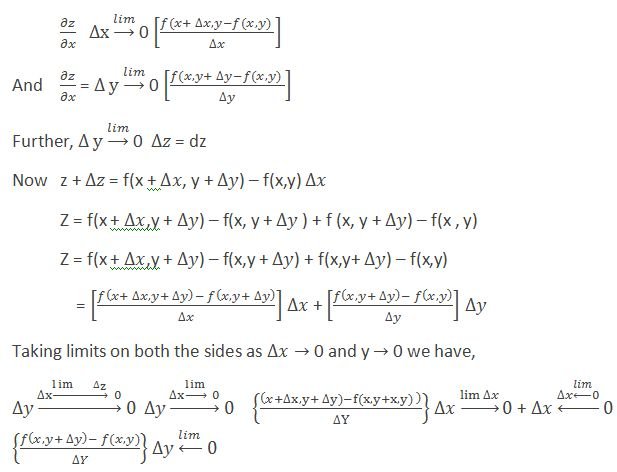Total Differentials

The partial derivatives ∂z/∂x and ∂z/∂y of the function z = f(x, y) measure the small variations in x or y. The total differential provides us with an idea of linear approximation of the small variations in the function z due to small variations in both x and y.

The symbols dx and dy in the derivative dy/dx of the function y = f(x) are calledthe differentials. The differential of y is defined as:

Dy = f’ (x) Δx

Then, the differential of dx of x is given by

dx = 1Δx

Since derivative of x with respect to itself is 1. Thus, the equation (1) can be written as

Dy = f’ (x) dx

This concept can be applied to the function of two, or more variables. Let z = f(x, y) be a function of two variables x and y. For small increments Δx and Δy in x and y respectively, let Δz be the corresponding increment in z. By definition we have,

Let dx, dy and dz be the limiting values of Δx, Δy and Δz. Then, from the above equation we get,

Dz = ∂z/∂x. dx +∂z/∂y × dy are called partial differentials of z with respect to x and y respectively. The sum of these partial differentials of a function is called the total differential.

The result of the above equation can be extended to the functions of several independent variables. Thus, when z = f(x, y, r) then,

dz = ∂z/∂x dx + ∂z/∂y dy + ∂z/∂r.