Algebraic Properties of Geometric Mean

Geometric mean, as a mathematical average, has a lot of algebraic properties.

Some of the important properties are depicted are depicted here as under:

1. For any series of positive values, the geometric mean is smaller than the arithmetic mean. However, when all the values of a series are equal, G.M. equals to the arithmetic mean.

Proof. Let a be the largest and b the smallest positive values of a series.

Then      (a –b)² > 0

So, a2 – 2ab + b2 > 0

So, a2 + 2ab+ b2 > 4ab     (adding 4ab to both the sides)

So,          (a + b)2 > (2√ab )²

So,          a + b > 2√ab,

So,  a+b/2 >√ab  , (Dividing each side by 2)

Now a+b/2 = Arithmetic mean and √ab = Geometric Mean

X > G and G < X

2.  If any value of a series is zero, the value of geometric mean is infinity and thus inappropriate.

Proof. Let there be 3 times viz. 15, 20 and 0. The geometric mean of these items would be

3√(15 x 20 x 0) = 3√0 = infinity, and hence inappropriate.

3. It can not be calculated, if the number of negative values is odd.This is because, the product of the values will become negative, and we can not find out the root of a negative product viz.

3√(-3 x -5 x -4 x 7) or 4√-420

4. Since, geometric mean or G = N√(X1. X2…..Xn),  the geometric mean raised to the nth power equals to the product of the values

i.e.          G^{n =}  X₁.X₂. X₃…X_n.

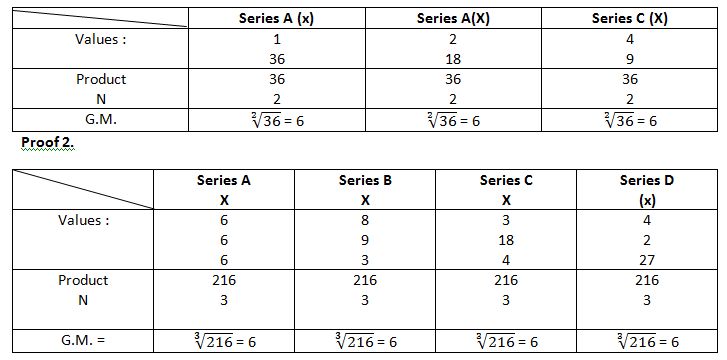
5.  Any series of numbers having the same N, and the same product will have same geometric mean.

6. The product of the ratios of the values on one side of the geometric mean is equal to the product of the ratios of the geometric mean to the values of the other side of the geometric mean.

Proof. Let 4,5,20 and 25 be the values of a series. The G.M. of the series would be 4√(4 x 5 x 20 x 25 = 10. Here, the values 4 and 5 are on one side of the G.M. 10 and the values 20 and 25 are on the other side of the G.M. 10.

The product of the rations of the of the values 4 and 5 to G.M.

(4/10) x (5/10) = 1/5

And, the product of the rations of the G.M. to the values 20 and 25.

(10/20) x (10/25) = 1/5

Thus, the two products are equal.

The product of the reverse of the above rations will also be equal.

The product of the reverse of the above of rations will also be equal.

Thus, (10/4) x (10/5) = 5, (20/10) x (20/25) = 5

7. The products of a series of numbers remain the same even when each number of the series is replaced by its geometric mean.

Proof. Product of the series, 4,5, 20,25 = 10000

Geometric mean of the series = 4√(4 x 5 x 20 x 25) = 10

If each number of the series is replaced by G.M.10, the series becomes 10, 10, 0, 10.

 The product of this series 10 × 10 × 10 × 10 = 10000. Proved.

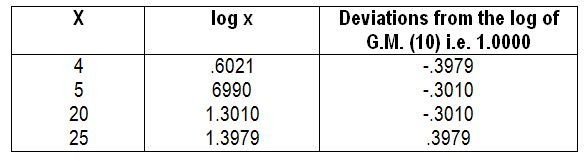
8. The sum of deviations of the logarithms of the original values above and below the logarithm of the G.M. is equal.

Here, sum of the deviations below G.M.

= .3979 + .3010 = .6989

And, sum of the deviations above the G.M.

= .3010 + .3979 = .6989

Note that the G.M. here =4√(4 x 5 x 20 x 25) = 10, and that its logarithm= 1.0000.