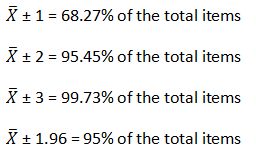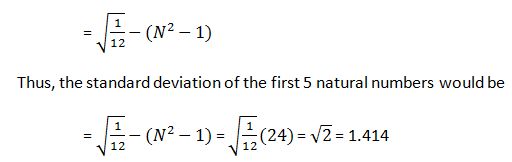Algebraic Properties of Standard Deviation
Standard deviation has a lot of algebraic properties for which it is capable of further algebraic treatment, and considered as the best of the measures of dispersion. Some of its algebraic properties are depicted here as under.
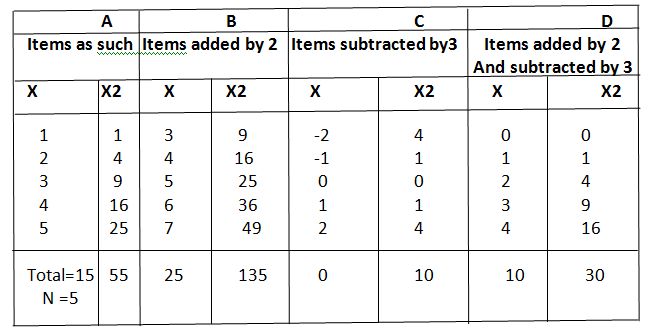
1. It is independent of change in the origin.This means that the value of the standard deviation will remain the same, even if, each of the items of a series is added or subtracted by a constant quantity.
Proof. Let there be 5 items in a series as 1,2,3,4 and 5. The standard deviations of these items as such and after of these items as such and after a change in their origin will be as under.
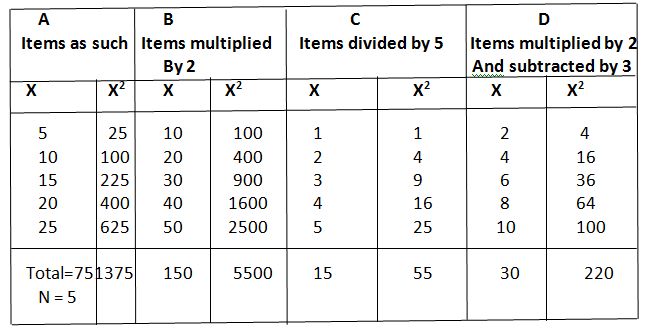
2.It is dependent of the change in the scale. This means that the value of standard deviation is multiplied, or divided by the same contact by which each item of the series is multiplied, or divided.
Proof. Let there be 5 items in a series as 5,10,15,20 and 25. The standard deviation of these items as such, and after the change in their scale will be as under.
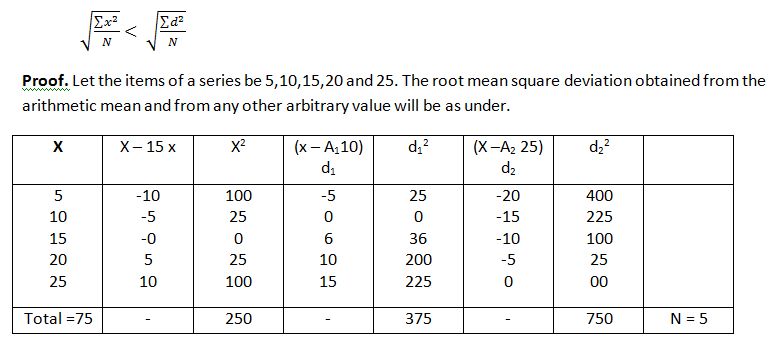
3. If is the minimum root mean square deviation because, it is calculated from the arithmetic average of a series and so.
4. In a symmetric and moderately asymmetric series, it maintains the empirical relation with the to there measures of dispersion as under:
Q.D = 2/3 , or .6745
M.D. = 4/5 , or.7979
Range = 6
5. It determines the number of items that fall within a specific range of a symmetrical distribution with the following relationships.
6. It is possible to determine the standard deviation of the natural numbers straight-way with the following formula