Characteristics of a Binomial Distribution
The essential characteristics of a binomial distribution may be enumerated as under:
1.For n trials, a binomial distribution consists of (n + 1) terms, the successive binomial coefficients being nC0,nC1,nC2,nC3 ,nCn-1, and nCn.
2. All the probabilities of a binomial distribution can be obtained, if n and p are known, the value of q being 1-p.
3. If p = q = 1/2, the distribution obtained would be symmetrical, and the expected frequencies on either side of the central value would be identical. Thus, when 4 fair coins are tossed 256 times, the frequencies for 4,3,2,1, and 0 heads would be, 16,64,96,64 and 16 respectively, which shows that the distribution is symmetrical. Even if, p ≠ q, the distribution would tend to be symmetrical. If n is increased sufficiently, otherwise the distribution would be skewed, or asymmetrical. Thus, in the above case, if p = ¼, and q = ¾, the expected frequencies would be 1,12,54,108 and 81 respectively.
4. A binomial distribution is positively skewed, if P ½ < 1/2 and it is negatively skewed if P >1/2.
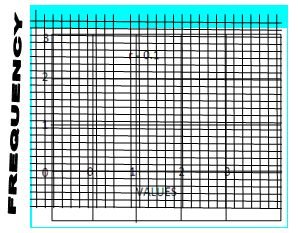
5. A binomial distribution can be very well graphically represented by showing the values of the variables along the horizontal axis in terms of possible numbers of success, and the probability of occurrences, i.e., the expected frequencies along the vertical axis.
6. The shape, and the location of a binomial distribution change as p changes for a given n, or as n changes for a given p. When p increases for a fixed n, the binomial distribution shifts to the right. This is shown by the diagrams as under:
7. The value of Mode of a binomial distribution is equal to the value of X which has the largest expected frequenc. The Mean and Mode are equal if np is an interger For example, when n= 6, and p= 0.5, the Mean and Mode are equal to 3 (i.e. 6 × 5). For a fixed n, both the Mean and Mode increase as p increases.
8. A binomial distrution is unimodal, if np is a whole number, i.e. an integer.
9. Since, the random variasble X takes only intergral values, a binominal distribution is discrete probability distribution.
10. As n increases for a fixed p, the binomial distribution moves to the right, flattens and spreads out. The Mean of the distribution obviously increases as n increases with p help constant.
11. If n is large, and if neither p, n nor q is too close to zero, the binomial distribution can be closely approximated by a normal distribution with a standard variable given by Z =x-np/√npq . The approximation becomes better with increasing n.