Co–efficient of Determination
Co –efficient of determination is, also, another measure of determining the correlation in the same manner as that of the Pearson’s co-efficient of correlation. This has been introduced by het famous Statistician, Tuttle who says that it is much easier to understand, and ver6y much useful for interpreting the results of the co-efficient of correlation between any two variables through the co-efficient of determination.
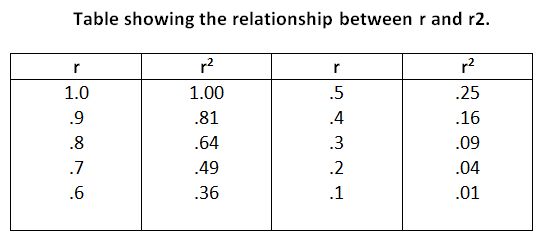
According to him, co-efficient of determination is nothing but the square of the Pearson’s co-efficient of correlation. i.e. r2. In other words, it is defined as the ratio of the explained variations to the total variations. Thus, if r = .8, r2 =,64, which would mean that 64 percent of the variations in the dependent variable has been explained by the independent variable, and the rest 36 percent of the variations is due to the other factors.
Co-efficient of determination is, therefore, represented as follows:
Co-eff. of Determination = r2 = Explained Variation/Total Variation
From the above formula it is to be noted that the value of the co-efficient of determination shall always remain positive, and its maximum value will be 1. As such, it cannot reveal if the correlation between any two variables is positive or negative. Further, it is to be noted that the value of r2 decrease more rapidly than the value of r and that the value of r will always be greater than the value of r2 as shown below: