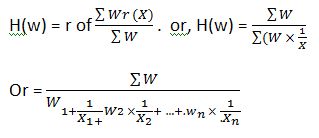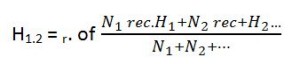Harmonic Mean

Harmonic mean is another mathematical average. It is defined as the “Reciprocal of the arithmetic average of the reciprocals of the values of a variable

Thus, the fundamental formula for its calculation in the different series are as follows:

H = reciprocal of  ∑rx/N or N/∑rx

Where, H = Hormonic mean

∑rx = Sum of the reciprocals of the variable or mid values

N = No. of observations or ∑F

The above formula can also be can also be modified as under:

Where, X1, X2, X3 etc. = Values of the variables

F1, F2, F3 etc.  = Frequencies of the respective variables

∑r_{(x)   =} Total of the products of reciprocals of the variables, and

And their corresponding frequencies.

All other factors carry the same meaning as before.

Weighted Harmonic Mean:

Further, for computing the weighted harmonic mean, the formula is to be modified as under:

Where, H(w) represents the weighted harmonic mean,

And ∑wr_(x),  the total of the products of the reciprocals of the values, and their corresponding frequencies.

Combined Harmonic Mean:

In order to compute the combined harmonic mean of two, or more series at a time, the formula is as under:

From the above definition and the different formula it follows that computation of harmonic mean depends entirely on the reciprocals of the values.