Hypothesis Testing
Hypothesis Testing
A hypothesis is the statement about relationships between variables or it is a tentative explanation for certain behaviours, phenomenon or events that have occurred or will occur. And to test its validity, statistical hypothesis testing is conducted.
In place, hypothesis testing specifies how to use a random sample to justify if it is the proof that supports or not the hypothesis.
Hypothesis testing is formulated in terms of two hypotheses:
H0: the null hypothesis;
- States the assumption (numerical) to be tested
- Begin with the assumption that the null hypothesis is TRUE
- Always contains the ‘=’ sign
H1: the alternate hypothesis.
- It is the opposite of the null hypothesis
- Never contains just the ‘=’ sign. Will have less than or greater than sign in it.
Types of errors:
The null and alternate hypothesis are two competing statements about the population. Either of them is true. But since the hypothesis tests are based on sample information, we must allow for the possibility for errors.
The possible outcomes are:
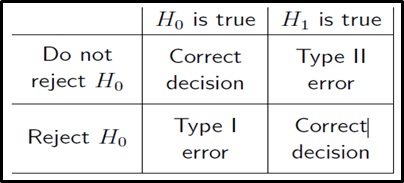
The acceptance of H1 when H0 is true is called a Type I error. The chances of executing a type I error can be stated as the levelof significance and is represented by ‘α’.
The lower significance level ‘alpha’, the less likely we are to commit a type I error. Generally, we would like small values of alpha; typically, 0.05 or smaller.
Failure to reject H0 when H1 is true is called a Type II error. The probability of committing a type II error is denoted by ‘ß’.It is impossible to compute ‘ß’ unless we have a specific alternate hypothesis.
