Kurtosis

(i)  Meaning and Purpose

Kurtosis is a statistical measure which is calculated on the basis of Moments to bring about another characteristic of a series. This characteristic refers to the flatness, or peakedness of the curve obtained from a series. A series, when plotted on a graph paper may produce either of the following three types of curves.

• Symmetric, or normal curve which is neither more flat nor more peaked.
• Asymmetric curve which is more flat than a normal one.
• Asymmetric curve which is more peaked than a normal one.

Thus, through the measure of Kurtosis we can know, if a distribution would give us a normal curve, a curve which is more flat than a normal one, or a curve which is more peaked than a normal curve.

It is to be noted that the word Kurtosis is a Greek word which means bulginess. Similarly, in Greek language, a normal curve is called Mesokurtic, a more flatted curve is called Platykurtic, and a more peaked curve is called a Leptokurtic. The sketches of these types of curves are given here as under:

 

Characteristics of the curves

From the above diagram, it must be seen that a Leptokurtic curve is more peaked than a normal curve. It has higher tails on the base but narrower space in the centre. A Mesokurtic curve is a normal one, which is neither too peaked nor too flat. Its tails on the base are neither too long nor too short, so also, it occupies a normal space in the centre. A platykurtic curve is more flat-topped than a normal one. It has very short tails on the base but broader space in the centre.

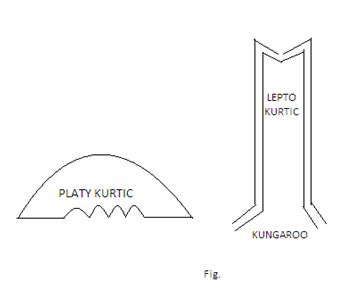
According to the famous British Mathematician W.S. Gosset (Student) Platykurtic curves, like the platypus, are squat with short tails, Lepto kurtic curves are high with long tails like the Kungaroos noted for leaping. To illustrate his statement, Gosset gives the following sketches of the Platy kurtic and Leptokurtic curves:

(ii) Definitions of Kurtosis

However, the measure of Kurtosis has been defined differently by various writers. Some such definitions are reproduced here, for a better understanding. Of the readers:

1. According to Simpson and Kafka, “The degree of Kurtosis of a distribution is measured relative to the peakedness of a normal curve.”
2. According to Spiegel, “Kurtosis is the degree of peakedness of a distribution, usually taken relative to a normal distribution.”
3. According to Croxton and Cowden, “A measure of skewness indicates the degree to which a curve of a frequency distribution is peaked or flat-topped.”

From all the above definitions, it must be clear kurtosis as a measure, refers to the flatness or peakedness of a curve obtainable from a distribution.

(iii) Different Methods of Kurtosis

There are two constants or co-efficients through which Kurtosis of a series is determined. They are (1)

β2 and (2) Y_2.

β2 (Beta Two)

According to Prof. Karl Pearson, Kurtosis of a series can be measured by  (beta two) which is equal to

μ4/μ2² or μ4/α4 or α4

Indications

If  β2 = 3, it will give a normal or a Meso kurtic curve.

If  β2 > 3, it will give a Lepto kurtic, or a more peaked curve.

If  β2 < 3 it will give a platy kurtic, or a more flat-topped curve.

2.  Y₂ (Gamma Two)

According to R.A. Fisher, kurtosis is measured by Y₂ which is equal to   _{β2 < 3}

Indications

If Y_{2 =} 0, it will give a meso kurtic or a normal curve.

If Y_{2 >} 0,  it will give a more peaked or a lepto kurtic curve.

If Y_{2 <} 0,  it will give a more flat-topped or a platy kurtic curve.

Usefulness of kurtosis

Among other things, kurtosis as a measure of statistics is particularly useful in the following matters:

• It is used for determining the type of curve a distribution is likely to produce i.e. meso kurtic, platy kurtic or lepto kurtic.
• It is used for selecting the suitable average for analysis of a series. If the distribution is a normal one, Mean is considered as the suitable average. If the distribution is lepto kurtic, Quartiles are taken to be suitable average for the analysis of the series.