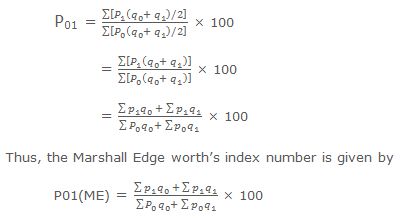Marshall and Edge worth’s Weighted Aggregative Method

The formula enunciated by Marshall and Edgeworth for constructing an index number is known as Marshall-Edge worth’s method. In this method, they have suggested to take the arithmetic average of the quantities of the quantities of the base year, and the current year as the weights of the items. Thus, the weight of an item would, be  . Accordingly, they have formulated the formula of index number as under:

Merits

This method commands the following merits:

• It is simple to understand, and easy to calculate.
• It gives a result which is approximately close to the results obtained by the Fisher’s ideal formula, and lies between the results of Laspeyre and Paashe’s indices.
• It makes use of all the data viz ; p₁,p₀,q₁, and q₀.
• It satisfies the time reversal test of consistency as the weights remain constant under this method.
• It also satisfies the unit test of consistency.

Demerits

• It needs current weights every time an index is computed.
• It needs all the data relating to price and quantities of both the base and current years for which the work becomes tedious and expensive.
• It does not satisfy the factor reversal test, and circular test of consistency.