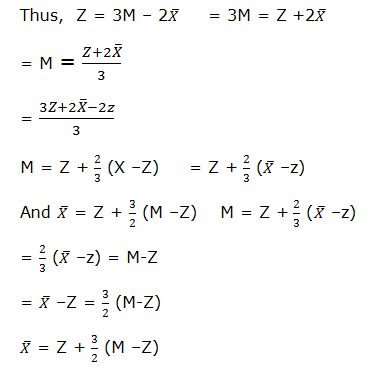Method of Empirical Relation

This is the last method of determining the value of a Mode from a series when all the aforesaid three methods fail in determining its value in a definite manner. This method has been propounded by Prf. Karl Person as the last resort of determining the mode. Through his experiments,

Proof.

Person found that in a moderately asymmetric or skewed serried; a pertinent relationship exists among the Mean, Median and Mode. In such series, the series, the distance between the Me4an, and the Median is almost 1/3 rd of the distance between the Mean and the Mode.

Thus, 1/3 (Mean – Mode) = Mean – Median

or   1/3  ( – Z) = (– M)

where, X represents mean M represents Median, and Z represents Mode. This relationship among the Mean, Median and Mode can be exhibited graphically as under:

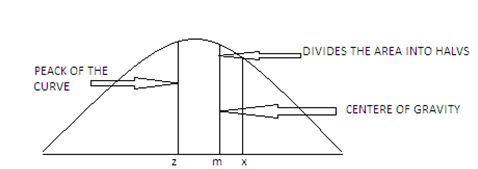
Graphic Representation of The Relationship Between Mean, Median And Mode

From the above diagram, it must be seen that Z > M >  and that   (Z –) = ( – M).

From such a relationship, Prof. Pearson observed that

Mode = Mean – 3 (Mean – Median)

or   Z = X – 3X + 3M

or Z = 3M – 2

Thus, Mode = 3 Median – 2 Mean

Further, on the basis of the above empirical relationship, the value of any of the three parameters viz. , M and Z can be computed, if the values of the other two parameters are given: