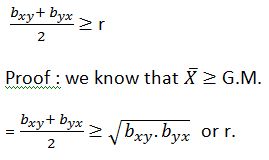Properties of Regression Coefficients

The regression coefficients explained as above have a number of valuable properties which may be cited as under:

Coefficients of correlation i.e.,

2. Both the regression coefficients must have the same algebraic sign i.e. both of them will have either + signs or – signs. This is because, minus sign with one coefficient will make the product of the two coefficients minus and in that case we cannot find out its square root to obtain the correlation coefficient. Thus, the first property mentioned above will be vitiated.

3. The nature of the regression coefficients is reflected on the nature of the coefficient correlation. This means that if the regression coefficients are positive the correlation coefficient will be positive, and if the regression coefficients are negative then the correlation coefficient will be negative. Thus if bxy = -5. and byx = -1.5, then r would be √-5 x -1.5 = -2=0.86 and not + 0.86.

4. If one of the regression coefficients is greater than unity (1), the other must be less than unity. This is because

r= √(b×y . byx) = ±1

and never greater than 1.

If both the regression coefficients happen to be more than 1, then their geometric mean will exceed 1 which will not give the correlation coefficient whose value never exceeds 1.

5. The arithmetic mean of the regression coefficients is either equal to or more than the correlation coefficient i.e

6. From the regression coefficients we can find out the value of any factor forming part of it, if the value of he other 3 factors are given. Thus, if we are given, r = 0.5,  = 3 and  = 0.6 we can find out the value of  as under:

7. Regression coefficients are independent of change of origin but not of scale. This means that if that if the original values of the two variables are added or subtracted by some constant, the values of the regression coefficients will remain the same. But if the original values of the two variables are multiplied, or divided by some constant (common factors) the values of the regression equation will not remain the same.