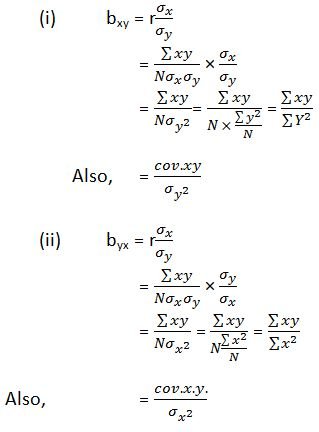Regression Coefficient

A regression coefficient is a vital factor that measures the change in the value of one variable with respect to a unit change in the value of another variable. From the above formula, it must be observed that the regression equation of X on Y is formed on the basis of its regression coefficient i.e. b_xy, or r x(Óx/Óy)  which measures the change in the value of X variable for a unit change in the value of Y variable. Similarly, the regression equation of Y on X is formed on the bases of its regression coefficient i.e. byx or, r x(Óx/Óy)  which measures the changes in the value of Y variable for a unit change in the value of X variable.

To simplify the process of finding the above two regression coefficients, the following formula may be substituted in place of the given ones:

• b_xy or b₁ = ∑xy/∑y² ; and
• b_yx or b₂=  ∑xy/∑x²

In the above formula,

b_xy or b₁ = regression coefficient of X on Y

by_x or b₂ = regression coefficient of Y on X

∑xy = total of the products of deviations of the X and Y variable from their respective actual Means,

∑xy = total of the squares of the deviations of Y variable from its actual Mean

∑xy = total of the squares of the deviations of the X variable from its actual Mean.

The above two simplified formula of the regression coefficients have been derived as under: