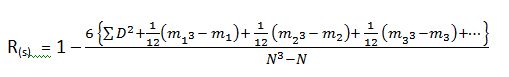Spearman’s Rank Correlation
This method is a development over Karl Pearson’s method of correlation on the point that (i) it does nto need the quantitative expression of the data, and (ii) It does not assume that the population under study is normally distributed.
This method was introduced by the British Psychologist Charles Edward Spearman in 1904. Under this method, correlation is measured on the basis of the ranks rather than the original values of the variables. For this, the values of the two variables are first converted into ranks in a particular order depicted as under:
Order of Assigning the Ranks
The ranks may be assigned to the different values either in ascending, or in descending order. In case of ascending order, the smallest rank 1 is assigned to the smallest value of a variable, and the subsequent ranks 2,3,4 etc. are given to the other values in order of their largeness in size. In case of descending order, the smallest rank 1 is given to the largest value of a variable and the subsequent ranks 2,3,4 etc. are given to the other values in order of their smallness in size. In whatever order, the ranks may be given, the same order of ranking must be followed in case of both the variables. When two, or more values of a variable are found to be identical, each of them is to be assigned with the average of their progressive ranks. For example, if there are three 30s coming after the 4th rank, their progressive ranks would be 5,6 and 7 respectively and their average would be (5+6+7)/3 i.e. Thus, each of the three identical values will be assigned with the rank6, and the next rank will begin with 8 to be assigned to the in next value of the series.
Method of Computation
After the ranks are assigned to the values of both the variables under the two columns R1 and R2 respectively, the squares of the differences between the two corresponding ranks are found out under the next column (R1 – R2)2 or D2. Lastly, the D2 column is totaled, and the following formula is put to find out the values of the co-efficient of correlation which also lies between ± 1.
Where,
R(s) = Spearman’s rank co-efficient of correlation
∑D² = Sum of the squares of the differences between the corresponding ranks of the two variables i.e.
∑(R1-R2)²
N = number of pairs of the two variables.
M1 = the number of items which are assigned with the first repeated rank.
M2 = the number of items which are assigned with the second repeated rank.
M3 = the number of items which are assigned with the third repeated rank.
Note. It is to be noted that when there is no repetition of any rank the above formula may be reduced as follows:
R(s) = 1 – 6∑D²/N³-N