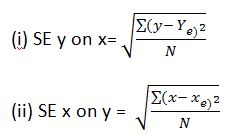Standard Error of Estimates

The regression lines or equations relating to the two variables are nothing but the limes or equations of estimates. With these equations or lines, we estimate the best probable value of one variable say x, on the basis of some given value of the other variable say, Y. But it must not be taken for sure that the values of a variable, which we obtain by such estimation line or equations, are perfectly correct. Estimation is after all a matter of estimation and never exact. There must be some difference between the exact values, and the values we estimate with the regression equations. This difference is called error. Thus, while prediction the values of a variable with such equations it will be wise on out part to state always the probable amount of the error in these estimates. This probable amount of error expected to be in the estimates is called standard error of estimates.

Since, there are two estimating lines, or equations i.e. of X on Y, and of y on X, we can calculate the standard errors for both these lines of estimates. This is calculate the standard errors for both these lines of estimates. This is calculated just in the manner of standard deviation. As the standard deviation measures the scatter, or dispersion of the items about their Mean, the standard error of estimates measures the deviations of the observed values of a variable from their estimated values.

Formula

There are different types of formulae for computing the standard error of estimates which may be noted as under:

1.Fundamental formula.The fundamental, or conceptual formula for obtaining the standard errors of estimates are as under:

Where SEy on x = standard error of the estimates of Y on X

SE x on y = standard error of the estimates of X on Y

Y = observed value of the Y variable

X = observed value of the x variable

Y_e = estimated value of the Y variable

X_e = estimated value of the X variable.

N = number of pairs of observations