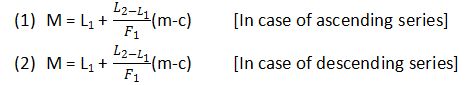Tabular Method of Mean

Under this method, the value of median is located from a table with the following model in the manner explained as under:

Formula

The fundamental model for determining the median is given by

M = Value of m or M = Value of  N+1 /2th item

N = Number of items arranged in an order.

In case of Individual and Discrete Series.

The above formula of median holds good in case of both individual, and discrete series. But in case of a continuous series, the following two types of formula are to be used in turn:

In case of Continuous Series

To find out the median item

M = Value of m, or

M = Value of N/2 th item

Here, m = median item i.e. N/2 th item

To Interpolate the Exact Value of Median

Where M = median

L₁ = lower limit, and L₂ = upper limit of the median class,

f1 = frequency of the median class,

m = median item i.e. N/2th item, and

c = cumulative frequency of the class that precedes the median class

Steps for Determination of Median

1. First, arrange the series in a table in ascending or descending order if it is given otherwise.
2. Then, find out the cumulative frequencies in a separate column headed by CF.
3. Then, find out the median item by applying the formula   N+1/2 [ N/2 In case of continuous series]
4. Then, locate the value of the median (median class in case of a continuous series) in the value column with reference to the median item in the cumulative frequency column.
5. In case of a continuous series, from the median class so located, determine the value of the median by applying any of the formula of interpolation cited as under: