Types of Event
An event connected with the theory of probability may be any of the following types : (1) Sure event, (2) Impossible event, (3) Random event (4) Elementary event, (5) Simple event, (6) Compound event, (7) Independent event (8) Dependent event, (9) Mutually exclusive event, (10) Overlapping event, (11) Equally likely event, and (12) Complementary event.
Each of the above types of events is explained here as under:
(1) Sure Event. An event which is sure to take place when a random experiment is performed is called a sure, or a certain event.
(2) Impossible Event. An event which can never take place when an experiment is performed is called an impossible event.
(3) Random Event. An event, the occurrence of which is uncertain or contingent is called a random or a contingent event.
(4) Elementary Event. An element of a sample space which represents all possible outcomes of a random experiment is called an elementary event. Thus every sample point is an elementary event.
(5) Simple Event. A single event the probability of occurrence of which is under consideration is called a simple event. The probability of such an event is represented as P (A) where ‘A’ represents event.
Compound Events. Two or more event which occurs jointly, and the probability of joint occurrence of which is under consideration is called a simple event. The probability of such an event is represented in any of the following forms:
P (A & B), or P (A ∩ B), or P (AB), or P (A). P (B)
Here, A and B represent two different events.
(7) Independent Event. An event the occurrence of which does not depend upon the occurrence of any other event is called an independent event. Thus, the results of tossing a coin, rolling a die, or drawing a ball each time after replacement of the ball drawn earlier are examples of independent events. In such cases the probability of the subsequent events are not affected by the occurrence of their preceding events. Thus the probability of getting a 5 upward in the 3rd trial of rolling a die will remain the same 1/6 as it was in the 1st and 2nd trials. Similarly, the probability of drawing spade card from a pack of 52 playing cards in the 2nd drawal will remain the same ,i.e., (13 spades/52 total) as it was in the first draw, provided the card drawn in the first draw is replaced before the second draw is made.
(8) Dependent Event. A subsequent event, the probability, or occurrence of which is affected by the probability, or occurrence of its preceding event, or event is called a dependent event. Thus, when the cards are drawn consecutively without replacement from a pack of 52 playing cards, the probability of drawing a spade in the 2nd draw will be (12/52) while in the first draw it was (13/52)
(1) Here, the probability of the second draw has been affected by the draw of a spade card in the first draw which was not replaced before the second draw thereby decreasing both the fovourable number of spade cards, and the total number of all the cards by one.
It is to be noted that no initial event can be a dependent event.
(9) Mutually Exclusive Events. Two or more events are taken as mutually exclusive, if the happening of one excludes or prevents the happening of another at the same time. Thus, with the tossing of a coin, either a head can come up, of happening of such events is expressed as P (A ∩ B), or P ( A or B ) exhibits the nature of two mutually exclusive events:
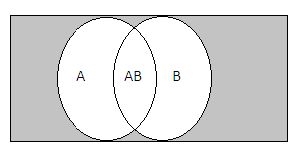
(10) Overlapping events. Two or more events that can take place together are called overlapping, or not-mutually exclusive events. The nature of such events can be exhibited diagrammatically as under :
The probability of happening of such events is represented by P (A B).
(11) Equally Likely Events. Two or more events are said to be equally likely, if each of them has the equal chance of happening, and none of them is expected to occur more often than the other. Thus in tossing of a coin, or rolling a die, all the outcomes, viz., H and T, or 1,2,3,4,5 and 6, are equally likely events, if the coin, or the die is an unbiased one.
(12) Complementary Events. Two events are said to be complementary to each other, if they are mutually exclusive and exhaustive as well. Thus, when a die is rolled, the outcome of an even number (2, 4 or 6) will be complementary event to the outcome of an odd number (1, 3 or 5).