Types of Probability

There are different types of probability which are briefly identified here as under:

(i) Prior Probability: It is also known as the classical or mathematical probability which is associated with the games of chance viz, tossing a coin, rolling a die, drawing a ball etc. The value of such a probability can be stated in advance by exprectation without waiting for the experiments as long as each outcome is equally likely to occur. The value of such a probability is calculated by the following simple formula:

1 P (E) = Number of favourable cases/Total Number

(ii)Empirical Probability: It is also otherwise known as a statistical probability which is derived from the past records. It is used in practical problems, viz., and computation of mortality table for a Life insurance company. The formula of computing such probability is as follows:

P (E) = Total number of occurrence of hte event/ total number of trials

For example, if the total number of persons insured at the age of 20 Years is 500 and the number of such persons dying was found to be 200, the empirical probability of the death is given by

P (E) =200/500 = .04

It is to be noted that when the number of observations is very large, the empirical probability of an event is taken as the relative frequency of its occurrence, and that such probability is equal to the prior probability.

(iii)   Objective Probability: A probability which is calculated on the basis of some historical data, common experience, recorded evidence, or rigorous analysis is called objective probability. Probabilities of various events in rolling of dice, or flipping of coins are examples of objectives probability in as much as they are based on dependable evidences.

(iv)   Subjective Probability: A probability which is calculated on the basis of personal experience or opinion is called a subjective probability. Probabilities of earning super profits for 10 years are the examples of subjective probability in as much as such probabilities are calculated purely on the basis of personal opinion of some experts.

(v)  Conditional Probability: The probability of a dependent event is called a conditional probability. If there are two dependent events, say A and B the conditional probability. If there are two dependent events, say A and B the conditional probability of A given that B has happened is given by ;

P (A/B) = P (AB)/P (B)

And the conditional probability of B given that A has happened is given by

P (B/A) = P (BA)/P (A)

Where P (AB) = P (A) × P (B/B)

Or  = P (B) × P (A/B)

If there are three dependent events say A, B and C:

P (ABC) = P (A) ×P (B/A) x P (C/AB)

Which represents that the probability of A, B and C is equal to the probability of A times the probability of B given that A has happened, B times the probability of C given that both A and B have happened.

It is to be noted that where conditional probability is attached to the two independent events say A and B, the conditional probabilities of A and B will be represented thus:

P (A/B) = P (A)

And   P (B/A) = P (B)

(Vi) Joint Probability: The product of a prior probability and a conditional probability is the joint probability of any two dependent or independent events. This is represented by P (AB), or P (A  B), or P (A). P (B/A), or P (B). P (A/B)

The values of joint probabilities of any two events can be better represented through a table known as the Joint Probability Table in which the intersection of the rows and columns are shown as the joint probabilities of the various events. The following examples would make the point very clear.

(Vii) Marginal Probability: This is, also, otherwise called as unconditional probability which refers to the probability of occurrence of an event without waiting for the occurrence of another event. The marginal probability of the events, say, A and B are represented as follows:

Marginal Probability of A = P (A) = m/m+n

Marginal Probability of B = P (B) = m/m+n

In a joint probability table, the marginal probability of an event can be easily calculated by adding the two joint probabilities relating to an event both row and column-wise. It is to be noted that sum of the marginal probabilities of all the related events will be equal to one. All these have been shown in the joint probability tables as solution to the illustrations 19 and 20 above.

Interrelationship between the Conditional, Joint and Marginal Probabilities:

All the three Conditional, Joint, and Marginal probabilities are inter-related with each other which can be seen from the following model:

P (B/A) = P(AB)/P(A)

Where,

P (B/A) = Conditional probability of B given that A has happened,

P (AB) = Joint probability of A and B

And P (A) = Marginal probability of A.

(Viii) Bayesian Probability: This probability is known is known is different names, viz., Posterior probability, Revised probability, and Inverse probability. This has been introduced by Thomas Bayes an English mathematician in his work known as Bayesian Decision Theory published in 1763. This theory consists of finding the probability of an event by taking into account of a given a sample information. Thus, a sample of 3 defective items out of 100 (event A) might be used to estimate the probability that a machine is not working properly (event B).

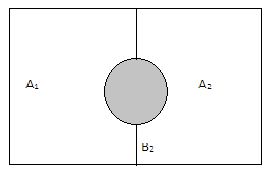
It is to be noted that the Bayesian Probability is based on the formula of conditional probability where, A1 and A2 are two events which are mutually exclusive and exhaustive, and B is a simple event which intersects each of the A events as shown in the following Venn diagram.

This is called posterior probability because; it is calculated after information is taken into account. This is called revised probability as it is determined by revising the prior probabilities in the light of the additional information gathered. Further, this called inverse probability also, as it consists of finding the probability of a probability.

However, the Bayesian, or the Posterior probabilities are always conditional probabilities which are calculated for every events as follows:

Posterior Probability = Joint Probability of the event of A/ Total of joint Probabilities of all

Of any event of A events of A, or Marginal probability of

Another event B.

Joint probability is the product of prior probability of an event of A and conditional probability of another event B, i.e., B/A.

Thus,  P(A₁) = P(A₁) x P(B/A₁)/P(B)

P(A₂) = P(A₂) x P(B/A₂)/P(B)

P(A₃) = P(A₃) x P(B/A₃)/P(B) and so on.