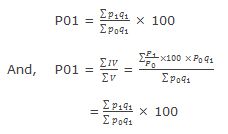Weighted Relative Method

This method is popularly known as the weighted price relative method, or Family budget method. Under this method, index number is computed by the following formula:

P₀₁ = ∑iv/ ∑v, Or ∑pv/ ∑v Or ∑pw/ ∑w

Where, P₀₁ = Price Index of the current year w.r.t. the price of the base year,

I = Index of price, or price relative i.e. (P_1/P_{0) X 100}

and P_{01 =  ∑iv/ ∑v} 

But, where V is taken as equal to P₀ × q₁, the result obtained by this method using the arithmetic mean equals the result that is obtained under Paasche’s aggregate method. This is because, the two formula equate as under:

Which is Paasche’s formula shown as above.

When geometric mean is used, the above formula of weighted price relatives, and their respective weights.

Merits

• This method commands the following merits:
• It is easy to understand, and simple to calculate.
• It allows the use of both arithmetic and geometric means.
• It allows the construction of different index numbers with a common base in a combined manner.
• It is flexible in the sense in the sense that the old items may be easily replaced by the new ones.
• The price, or quantity relatives of each of the items shown under this method serve themselves as the index numbers.

Demerits

• This method suffers from the following demerits:
• The computations work becomes tedious when geometric mean is used.
• There is no definiteness as to the manner of weighting.
• It does not satisfy the time reversal test and factor reversal test which are most important tests of consistency of a formula of index number.